Так как все виды помех вызываются работой электроустановок потребителей, совместное воздействие которых определяет суммарный вид уровень помех в точке общего присоединения, а ГОСТ 13109-97 устанавливает нормы только на суммарный уровень, возникает необходимость суммирования помех данного вида в данной ТОП.  В качестве такой ТОП обычно рассматриваются шины i—й подстанции, к которым в общем случае присоединяются несколько потребителей. (рисунок 1) [1].

Показатели КЭ вида K_U, K_U(n), K_2U, K_0U,характеризуют влияние  электроприёмников потребителя на качество электроэнергии в рассматриваемом узле системы. Значение ПКЭ в i—мопределяется токами искажений I_j, создаваемыми потребителями во всех узлах, так, что искажение напряжения в i—м узле (U₁) равно векторной сумме падений напряжения ∆U_I от этих токов на собственных (Z_ii) и взаимных (Z_ij) сопротивлениях, присоединенных к i—му узлу. Таким образом, для рисунка 1.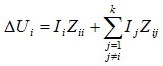

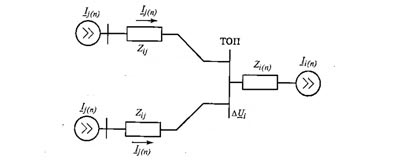
Рисунок 1 — Суммирование высших гармоник тока n-го порядка в СЭС с несколькими источниками.

Первое слагаемое этого выражения представляет собой искажение напряжения, вызываемое источниками несинусоидальности и несимметрии со стороны i—го источника. Второе слагаемое является суммой искажений, вносимых в i—ый узел источниками того же вида, установленными в j-х узлах сети. При этом следует иметь ввиду, что один и тот же элемент системы электроснабжения характеризуется разными сопротивлениями Z_ii и Z_{ij ,} которые имеют разные значения для токов n-ой, гармонической, обратной, нулевой последовательности.

Приведенное выше уравнение представляет собой векторную сумму, слагаемые которой изменяются случайным образом так, что их модуль может изменяться от 0 до 1, а аргумент от 0 до 2π. В частном случае это может быть и арифметическое сложение.

При вычислении допустимого вклада источника, когда уровень помех, создаваемых несколькими источниками, определяют расчетами, векторное суммирование заменяют «взвешивающими» показателями степени а.

Обозначив показатель степени, характеризующий механизм суммирования, через а, общую формулу для суммарного уровня искажения П конкретного вида можно представить в виде 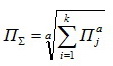, где k –число источников искажения.

Тогда векторы несимметрии напряжения по обратной и нулевой последовательности, распределяющиеся случайным образом, суммируются в квадратуре так, что

Колебания напряжения, создающие фликер, не являются векторными величинами. Их воздействие нормируется как накапливающееся влияние энергии светового потока. Поэтому воздействие источников колебаний напряжений суммируется арифметически.

Механизм суммирования высших гармоник, генерируемых преобразователями, установлен на основе экспериментальных исследований в зависимости от порядка гармоники:

• Для 3, 5, 7-й гармоник – арифметически, т.е. так. что для кривой напряжения, содержащей 3, 5 и 7-ю гармоники K_UΣ равен (при а=1):

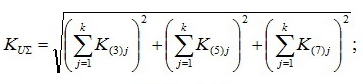
Для 11-й и 13-й гармоник в степени 1,4 (а=1,4):

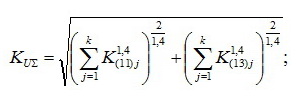
-для остальных гармоник во второй степени (a=2):

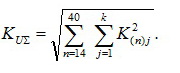
Показатель степени а, с которым суммируются гармоники, генерируемые преобразователями, расположенными в различных точках системы электроснабжения, на практике принимается равным «взвешенному» значению в зависимости от пульсности преобразователя, с учетом снижения амплитуд гармоник при увеличении их порядка. Тогда для 6-пульсных преобразователей, генерирующих нечетные гармоники, начиная с 5-й, показатель степени а  = 1,3. Для 12-пульсных преобразователей, генерирующих нечетные гармоники, начиная с 11-й, показатель степени а = 1,6.

Для остальных типов нелинейных электроприемников, например дуговых печей, сварочного оборудования и др., показатель степени а = 2. Тогда для потребителей со смешанным составом электроприемников а = 1,3d₆ + 1,6d₁₂ + 2d_пр, где d_6,d₁₂,  d_пр  — соответственно доли мощности 6- и 12-пульсных преобразователей и других источников высших гармоник.

Список использованной литературы

1.Карташев И.И. Управление качеством электроэнергии / И.И. Карташев, В.Н. Тульский, Р.Г. Шамонов и др.: под ред. Ю.В. Шарова. – М. : Издательский дом МЭИ, 2006. – 320 с.: ил.